As a data analyst you are often tasked with finding out the impact of an intervention (action, campaign, product release etc.) on some KPI. It’s “easy” when you are able to set up an ab-test and measure incremental gain/loss between control- and test-group. Implementing ab-tests (aka. split-tests, randomized experiments or hypothesis tests) should always be the number one choice for trying to measure causal impact of an action. In my view one of the most important jobs of a data scientist is to evangelize ab-testing as one of the cornerstones of becoming data driven.
There are scenarios where implementing ab-tests is not possible, for example TV campaigns or mobile app releases. In this case it’s tempting to resort to looking at graphs of the KPI before and after the intervention. For example, if a TV campaign was aired in April 2014 one could compare the sales increases from March to April 2014. To get a grip on seasonality these could be compared to the sales increases from March to April in 2013 and 2012. This is most likely better than nothing. But the problem with this is that it doesn’t take into account developments that might have led to the number of sales in March and differences in absolute levels. For example, March sales were on a high level in 2013 because of a successful product launch and sales decreased in April 2013 by -x%. If sales increased slightly from March 2014 to April 2014 by y% than it’s tempting to say that the absolute effect is x+y%, which of course is wrong.
Another method could be to do time-series-analysis (e.g. in R: http://www.statmethods.net/advstats/timeseries.html) and try to “forecast” how sales would have looked like, if there wasn’t an intervention. The forecasted time-series could be seen as a synthetic control and once compared to the actual number of sales gives an estimate of the sales-impact the intervention had. The validity of this approach of course depends heavily on the quality of the time-series-analysis and forecast accuracy. But given a sufficiently accurate forecasting-model this approach is preferable to the simple “before-and-after” analysis described above.
In September Google published “CausalImpact”, which is a new open-source R package for estimating causal effects in time-series (http://google-opensource.blogspot.de/2014/09/causalimpact-new-open-source-package.html). The aim of the package is to solve the problem of estimating the effect of an intervention when an ab-test isn’t available. Simply put, it is based on the before mentioned approach of producing a synthetic control via time-series modelling. In addition to that, it incorporates control time-series which predict (correlate with) the outcome of the time-series in the period before the intervention to produce the synthetic control. For example if the above mentioned TV campaign was aired in April 2014 in Germany only, than adequate control time-series could be the number of sales in other countries, e.g. the US or Japan.
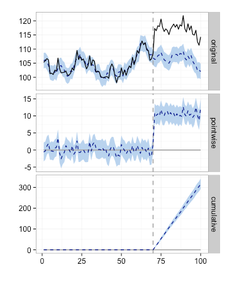
The plot on the left displays the result of the CausalImpact-package: Given an intervention at time point 71 the model predicts the expected time-series if there wasn't an intervention (the dotted line in the diagram labeled original).
The difference of the predicted (dotted line) to the actual time-series (solid line) is the effect of the intervention, which is displayed per time-point (pointwise) and cumulative.
It’s important to choose control variables that are not affected by the intervention. Choosing sales from countries such as Switzerland or Austria, which might have been impacted by the TV campaign Germany could result in invalid estimates.
This package is based on Bayesian structural time-series models and applies Markov chain Monte Carlo algorithms for model inversion. The paper is available here: http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/41854.pdf.
Validating ones assumptions is critical when doing this kind of causal analysis. As already mentioned, it’s important to check that the incorporated control time-series are not affected by the intervention. Secondly, one should understand how good this approach can predict the time-series in question before the intervention, in the TV campaign example the number of sales in Germany before April 2014. Using a fake intervention, say in March 2014, one would expect not to find a significant effect for this period, since there really was no intervention.
It’s probably tempting to only use this kind of approach and disregard ab-tests altogether. One could argue that the costs for implementing ab-tests might be higher. But I would always prefer an ab-test over doing time-series analysis. One of the many reasons is that ab-tests can control for external local impacts such as weather or special events, which this time-series-modelling can’t.
We used the CausalImpact-package to assess the effect of a recent TV campaign at Jimdo. Interestingly, the simple before- and after-comparison would have underestimated the impact compared to the analysis with the CausalImpact-package.

Write a comment
Sam (Wednesday, 28 October 2015 01:28)
Can you please share the code that you used to do the assessment of the TV campaign using CausalImpact package ? I was under the impression that I would not need to have a control while using CausalImpact package and that I could use it to create a Synthetic control. Please email me the code at saurabhsmit2004@gmail.com if possible.
Bob (Sunday, 30 April 2017 07:52)
Concise and clear. Thanks,
best essay writing service (Thursday, 07 September 2017 01:34)
Your article is very nice thank you for share this such a wonderful article. I am also getting more at essays and thesis papers.
Ay baba G (Thursday, 18 October 2018 08:21)
I am very glad to read this.
[url=https://www.kisssviss.com/]kisssviss[/url] (Thursday, 18 October 2018 08:24)
You are awesome
yuduzab (Thursday, 18 October 2018 08:24)
I am glad to read that you come up with outstanding information which definitely allow me to share with other.
<a href="http://www.abdulrazaq.com">Ay baba G</a>
"dkfjsdlf":http://www.coafsdmfs.com/ (Thursday, 18 October 2018 08:25)
Good to know tis.
www.assignmentgeek.com.au (Thursday, 18 October 2018 08:25)
Making trouble